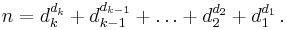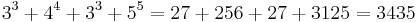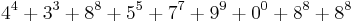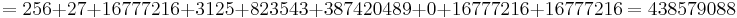Perfect digit-to-digit invariant

A perfect digit-to-digit invariant (PDDI) (also known as a Munchausen number^[1]) is a number that is equal to the sum of its digits each raised to a power equal to the digit.

$n = d_k^{d_k} %2B d_{k-1}^{d_{k-1}} %2B \dots %2B d_2^{d_2} %2B d_1^{d_1}\,.$

0 and 1 are PDDIs in any base (using the convention that 0⁰ = 0). Apart from 0 and 1 there are only two other PDDIs in the decimal system, 3435 and 438579088 (sequence A046253 in OEIS).

$3^3 %2B 4^4 %2B 3^3 %2B 5^5 = 27 %2B 256 %2B 27 %2B 3125 = 3435$

$4^4 %2B 3^3 %2B 8^8 %2B 5^5 %2B 7^7 %2B 9^9 %2B 0^0 %2B 8^8 %2B 8^8$

$= 256 %2B 27 %2B 16777216 %2B 3125 %2B 823543 %2B 387420489 %2B 0 %2B 16777216 %2B 16777216 = 438579088$

More generally, there are finitely many PDDIs in any base.

References

^ van Berkel, Daan (2009). "On a curious property of 3435". arXiv:0911.3038.